Números de Motzkin

Una imagen sin fecha del matemático estadounidense Theodore Motzkin.UNIVERSIDAD DE SAINT ANDREWS

La primera ilustración de la semana pasada, con sus líneas quebradas de distintos colores, no es un cuadro abstracto minimalista, sino la representación gráfica de los 63 caminos de Delannoy distintos en una cuadrícula de 3 x 3, o sea, D(3, 3). Y como señala Salva Fuster: “Para contar el número de recorridos monótonos en los que también podemos ir en diagonal, una de las imágenes del artículo puede ser de utilidad, pues la coloración depende del número de segmentos diagonales. Para cada caso (en función del número de segmentos diagonales), convendría utilizar permutaciones con repetición con los segmentos Norte y Este restantes”.

Y añade Luca Tanganelli: “En efecto, distinguiendo los casos según el número de segmentos diagonales da que D(m, n) = (m, n)(m – n, 0) + (m + 1, n – 1)(m – n + 2, 1) + (m + 2, n – 2)(m – n + 4, 2) +...+ (m + n, 0)(m + n, n)”.

Y señala Francisco Montesinos: “Como no hay marchas atrás, D(m, n) = D(m - 1, n) + D(m - 1, n - 1) + D(m, n - 1)”.

No hay una fórmula sencilla que dé el valor de D(m, n) en función de m y n; hay que recurrir a sumatorios, matrices o series infinitas. Y como cada número de Delannoy depende de dos enteros, no se puede listarlos linealmente, se requiere una tabla de doble entrada, denominada matriz de Delannoy.

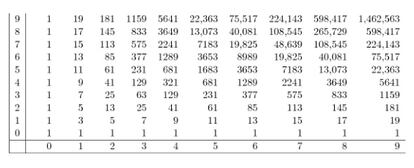
Obsérvese que D(0, 0) = 1, D(0, n) = 1, D(n, 0) = 1 para cualquier valor de n. ¿Cómo se justifica esto, dado que no hay cuadrículas de 0 filas o 0 columnas?

De las cuadrículas a los círculos

Si marcamos 4 puntos en una circunferencia, ¿de cuántas maneras diferentes podemos trazar cuerdas no secantes entre esos puntos? Si contamos también la opción de no trazar ninguna cuerda, hay 9 posibilidades: 1 con 0 cuerdas, 6 con 1 cuerda y 2 con 2 cuerdas.

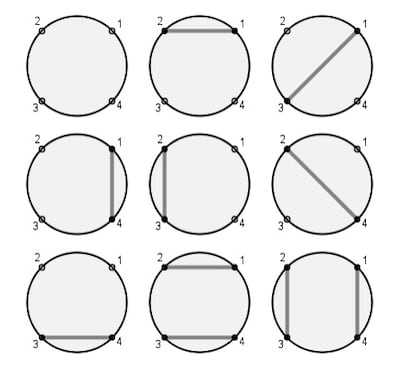
Obsérvese que no es posible trazar 3 cuerdas sin que ninguna se corte, por lo que 0, 1 y 2 cuerdas son, con 4 puntos, las únicas posibilidades.

Con esta construcción hemos hallado el cuarto de los números de Motzkin (llamados así en honor del matemático estadounidense Theodore Motzkin), correspondiente a 4 puntos. Si solo marcamos un punto en la circunferencia, solo tenemos la opción 0 cuerdas, por lo que el primer número de Motzkin es 1. Con 2 puntos, podemos trazar una cuerda o ninguna, por lo que el segundo número de Motzkin es 2. Con 3 puntos podemos no trazar ninguna cuerda o las 3 que unen los puntos dos a dos, por lo que el tercer número de Motzkin es 4. Y ya hemos visto que el quinto es 9. Tenemos, pues, la secuencia:

1, 2, 4, 9…

¿Cómo sigue? Me conformo con el quinto, pues el sexto es 51 y es bastante trabajoso dar con él. Y la secuencia crece rápidamente:

…51, 127, 323, 835, 2188, 5798…

Y la metapregunta de rigor: ¿por qué menciono los números de Motzkin después de hablar de los de Delannoy? ¿Qué relación hay entre ambos tipos de números?

Como curiosidad, los primos de Motzkin, o sea, los números de Motzkin que además son primos, han despertado el interés de los matemáticos a pesar de su escasez (o precisamente por ella). Hasta el momento solo se conocen cuatro:

2, 127, 15511 y 953467954114363.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.